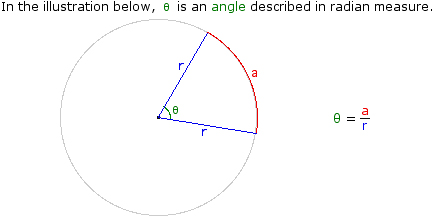
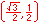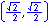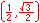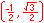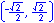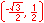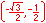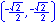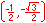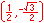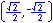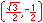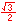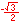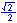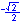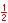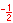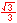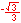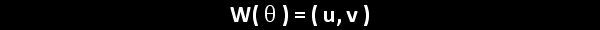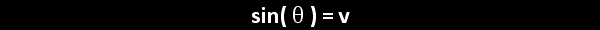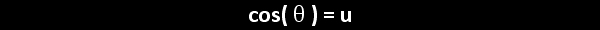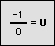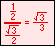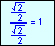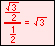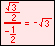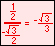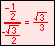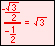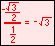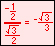Radian measure is the ratio of the length of a circular arc (a) to the radius of the arc (r).
Since radian measure is the ratio of a length to a length, the result is a pure number that needs no unit symbol. Most mathematicians do not write a unit attached to this ratio, although some people add the unit "radians" (symbol: "rad"), to indicate an angular measure, or length along a unit circle.
When no symbol is used, radians are assumed. When degrees are the unit of angular measure, the symbol "°" is written.
Note that the radian is a derived unit in the International System of Units (SI).
Note also that degrees is a unit outside the International System of Units (SI), but is accepted for use within SI.
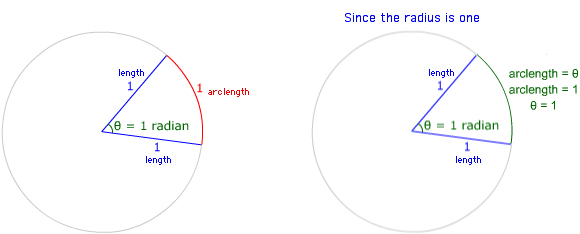
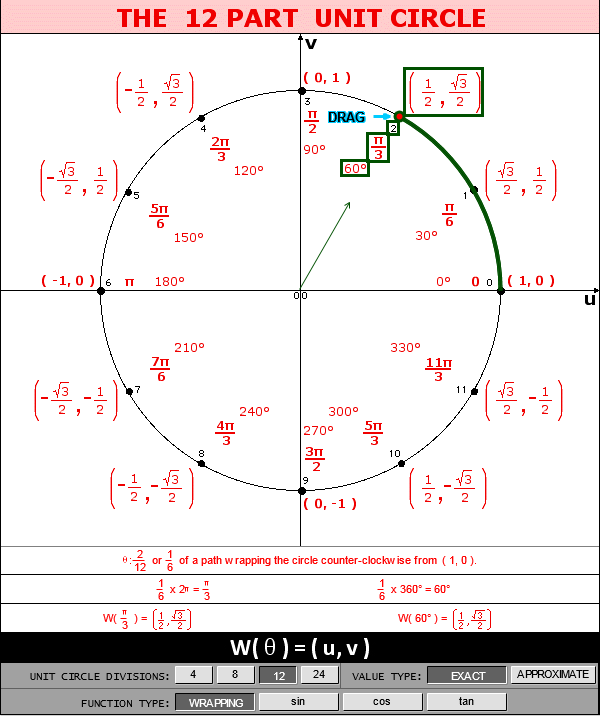
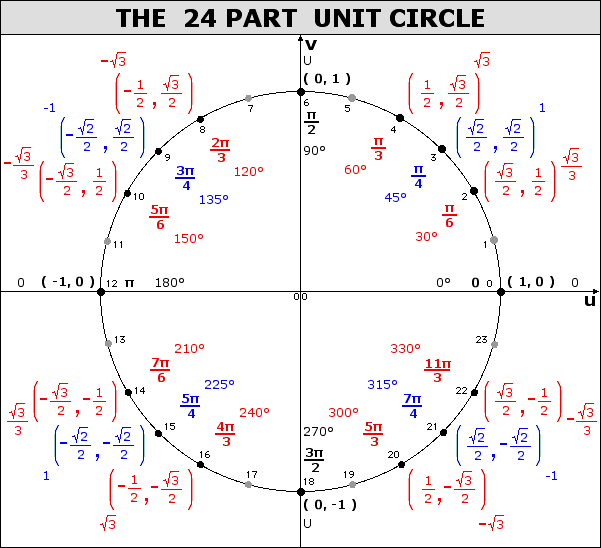
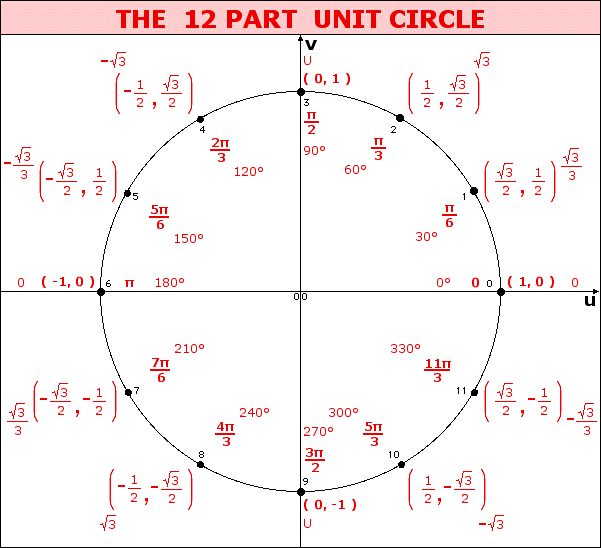
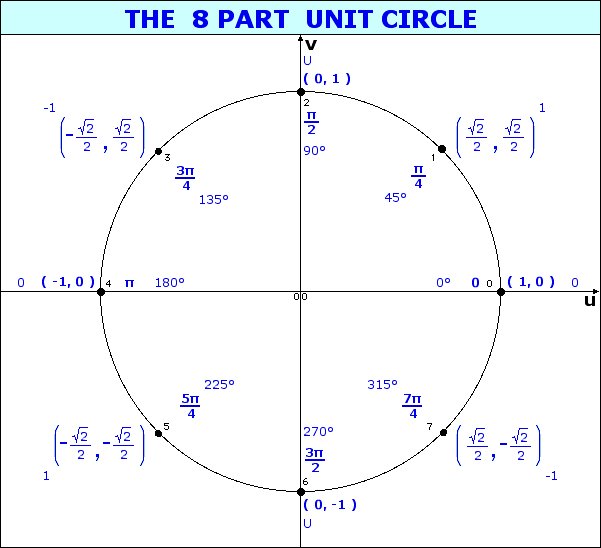
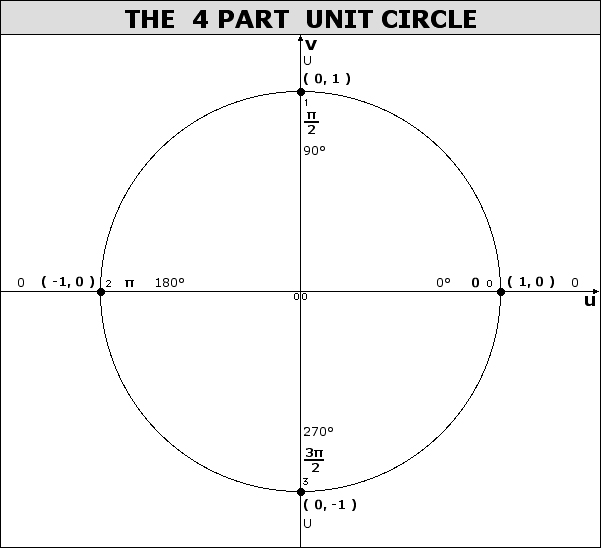
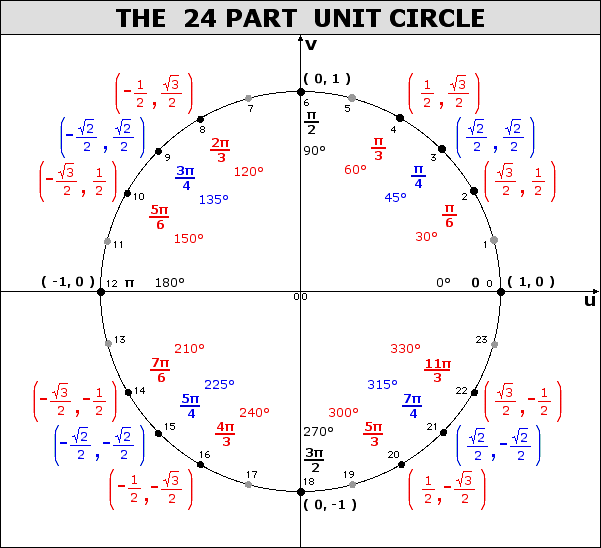
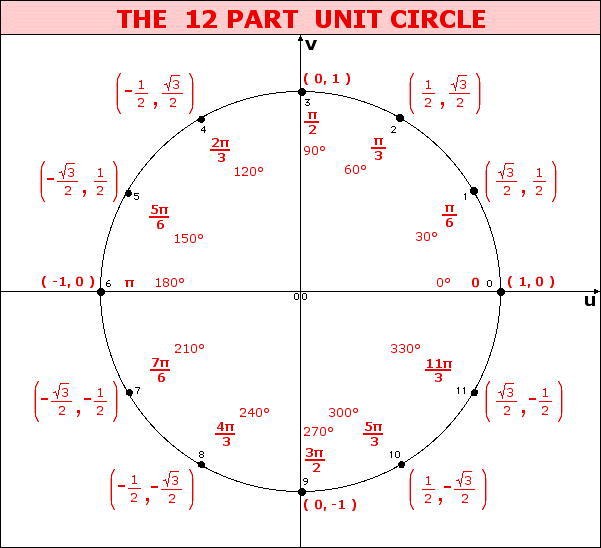
When dealing with a central angle of a unit circle, the measure of the angle (in radians) can be modelled as an arc length along the unit circle.
When looking at angle measure, the three measures of "one revolution", "2π", and "360°" are all equivalent, as are the three measures of "one-half revolution", "π", and "180°", etc.

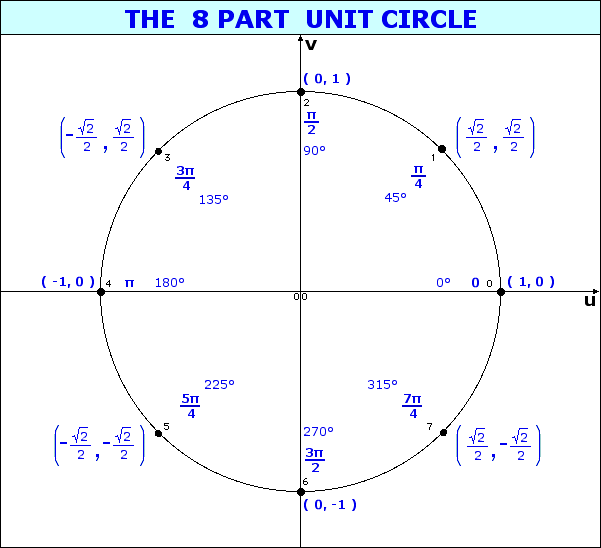
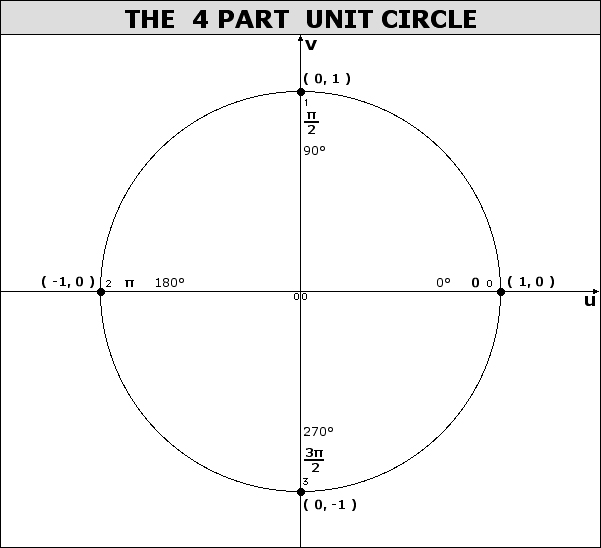
.gif)
.gif)
.gif)
.gif)